Seven Puzzle
Time Limit : 1 sec, Memory Limit : 65536 KB7パズルは8つの正方形のカードとこれらのカードがぴたりと収まる枠を使って行います。それぞれのカードは互いに区別できるように、0,1,2....7と番号がつけられています。枠には、縦に2個、横に4個のカードを並べることができます。
7パズルを始めるときには、まず枠にすべてのカードを入れます。枠のなかで0のカードだけは、上下左右に隣接するカードと位置を交換することができます。たとえば、枠の状態が図( a )のときに、0のカードの右に隣接した、7のカードと位置を交換すれば、図( b )の状態になります。あるいは、図( a )の状態から0のカードの下に隣接した2のカードと位置を交換すれば図( c )の状態になります。カードの位置を入れ替える操作はこれだけが許されます。図( a )の状態で0のカードと上下左右に隣接するカードは7と2のカードだけなので、これ以外の位置の入れ替えは許されません。
ゲームの目的は、カードをきれいに整列して図( d )の状態にすることです。最初の状態を入力とし、カードをきれいに整列するまでに、必要な最小手数を出力して終了するプログラムを作成してください。ただし、入力されたカードの状態からは図( d )の状態に移ることは可能であるとします。
入力データは、1行に8つの数字が与えられます。これらは、最初の状態のカードの並びを表します。図( a )の数字表現は0,7,3,4,2,5,1,6に、図( c )は2,7,3,4,0,5,1,6となります。
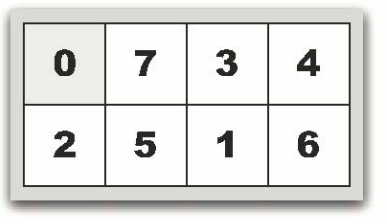 | 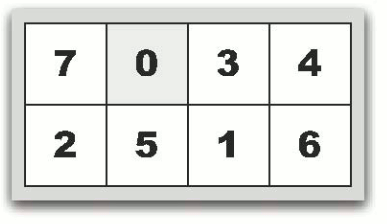 |
| 図( a ) 0,7,3,4,2,5,1,6の場合 | 図( b ) 7,0,3,4,2,5,1,6の場合 |
|---|
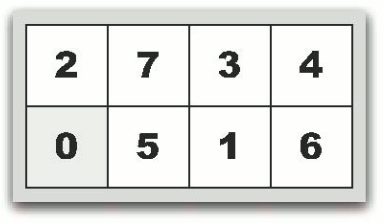 | 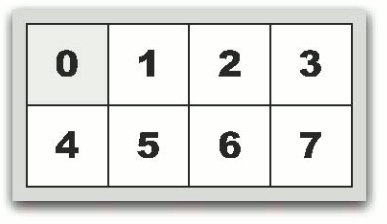 |
| 図( c ) 2,7,3,4,0,5,1,6の場合 | 図( d ) 0,1,2,3,4,5,6,7(最終状態) |
|---|
Input
1つ目のパズルの状態(整数;空白区切り)2つ目のパズルの状態(整数;空白区切り) : :
与えられるパズルの数は1000以下です。
Output
1つ目のパズルの状態から最終状態へ移行する最小手数(整数)2つ目のパズルの状態から最終状態へ移行する最小手数(整数) : :
Sample Input
0 1 2 3 4 5 6 71 0 2 3 4 5 6 77 6 5 4 3 2 1 0
Output for the Sample Input
0128 题意: 给个初始状态为0-7的一个排列,0表示空格。可以挪动空格周围的数字,最后使得最终状态为0-7顺序排列。 分析: 就是类似八数码的问题。之前没做过八数码的题。 记录下思考过程。 首先很容易想到就是从初始状态开始搜索出最终状态,每次的策略就是移动0周围的 数字。但,怎么表示状态呢?这8个格子不是可以看成矩阵用二维数组记录吗?于是。。。 1、可以用一个结构体,结构体中有一个二维数组来记录,另一个变量记录初始状态搜到的步数 2、结构体中的数组可以用一维数组,这样策略就是0所在的位置p与p+1、p-1、p+4、p-4四个位置 的元素交换,当然交换的pos位置必须在0-7范围内,且 换行的地方要注意!!! p=3时,pos=4是不行的 p=4时,pos=3是不行的 然后就是bfs搜了。 状态有8!(8个数全排列)= 40320 开始用的sum(a[i]*i)来hash,总是从7 6 5 4 3 2 1 0搜不到目标状态。 后来意识到是hash的时候有重复造成的错误! 于是看了下康托展开: 康托展开是一个到一个的,常用于构建时的空间压缩。 康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。 于是改写了hash方法后,能过样例了。。。 但是tle 于是把之前所有用vector的地方都改成了手写数组int a[8]。。 还是tle 于是想到预处理,从0 1 2 3 4 5 6 7这个排列作初始状态出发来搜, hash[i]记录到达i对应的排列的步数 n位(0~n-1)全排列后,其康托展开唯一且最大约为n!,因此可以由更小的空间来储存这些排列。 所以hash数组只要开8!+1=40321即可! OK!


1 #include2 #include 3 #include 4 #include 5 #include 6 #include 7 #include 8 #include 9 #include